Adding IMU acceleration

So far, our Kalman filter only used one element of data provided by IMU sensor: orientation. It was the easiest bit of data to integrate into the filter, as it requires no transformation between what sensor returns and what goes into robot's state.

Acceleration (ax, ay; we still ignore z for now) is different. Robot's state does not include acceleration (we can add it, but let's say we do not want it). More than that: the Hx() function in our code should take state and return expected sensor data. There is no way to get acceleration from x, y and theta! So we need to do something about it.

An obvious solution is to keep previous state of a robot. And as we keep it elsewhere (not in robot's state itself), we can also keep speed (one we received as a command input). As the result, at any point we will have current and previous speed (separated by time period dt), so we can calculate acceleration.

Here is another problem. The move() function that we use to model the robot's position, should update those stored data from the previous step. However, the move() is also called from Kalman filter itself - few times during each step! So we need to make sure it only updates once, when the next step (cycle) happens. This is done using cycle counter.

Now we are ready to take a look at the code of kalman_1_accel.py:

Now, let's test the filter.

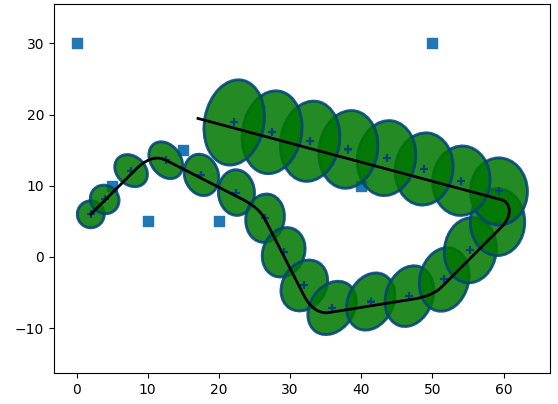
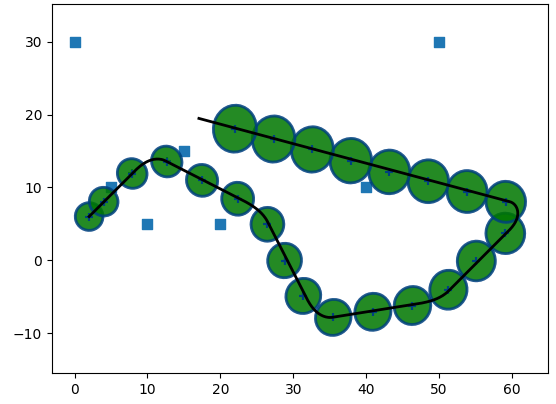
Note that the implementation is not complete. I still have to add IMU angular velocity, plus the way acceleration is used is a bit wrong. The filter itself is fine, but the way I provide data to it (the model of a sensor) assumes that "linear acceleration" only occures when we, well... linearly accelerate. Which is wrong.

If a robot with an IMU (Inertial Measurement Unit) sensor is moving in a circular path at a constant speed, the linear acceleration reported by the IMU will be non-zero. When an object moves in a circular path, even at a constant speed, it experiences a centripetal acceleration directed towards the center of the circle. This centripetal acceleration is necessary for the object to continuously change its direction and follow the curved path.

So we need to make sure we account for this when we pass simulated accelerations to Kalman filter. I will return to it later.