Practical Sensor fusion

Accelerometer

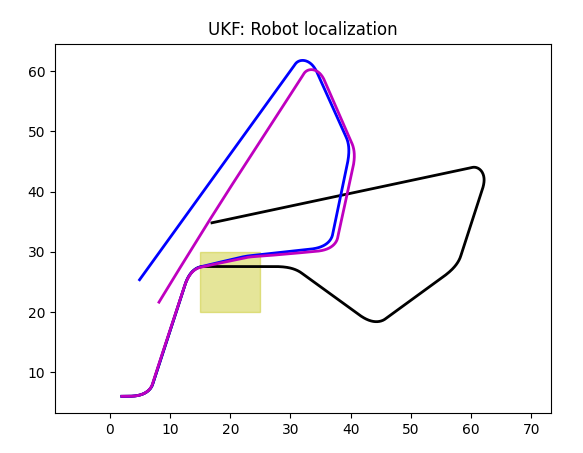
As follows from its name, accelerometer provides us accelerations. We can integrate it twice to get coordinates, but they will be noisy, as integration accumulates errors. Here we have a model of a cheap accelerometer, but it is still not that bad. And yet the error is large.

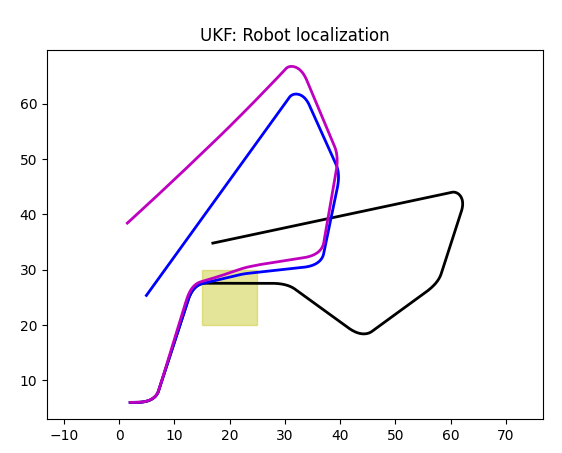
Here black line is an ideal trajectory without slippage. However, two slippery areas (yellow rectangles) are present, though robot only moves over one of them. So blue line is a real world (ground truth) trajectory with slippage, this is how robot really moved.

Magenta is a Kalman's prediction, as you can see, it tries to follow the blue line, but has signifficant deviation.

GPS

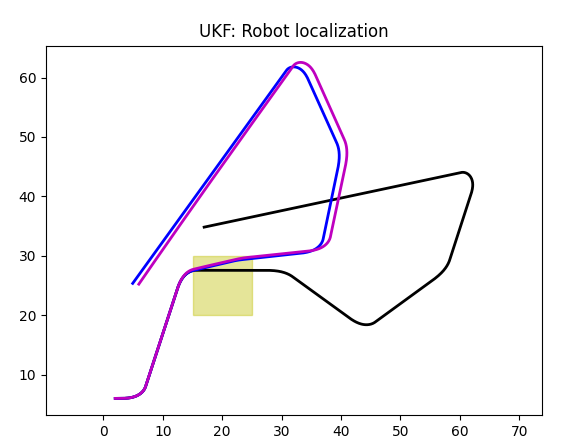
In our simulation, GPS std dev is set to 10 meters. This is a reasonable value for a customer level GPS receiver:

Here Kalman filter prediction follows real life (blue) trajectory reasonably well; the deviation is less than error of the GPS sensor (10 m).

Accelerometer plus GPS

Let's use accelerometer and GPS sensors together. What will happen?

It looks that quality of Kalman trajectory slightly increased. So how comes that accelerometer's deviation was compensated?

This probably is the most important thing to notice about the code, so please pay attention.

When I introduced slippage, I had to add compensation terms to the robot's state. Same terms work here: as soon as Kalman filter gets two sources of data plus command, it is able to figure out what and to what extent should be compensated. In some publications you will find people adding bias terms to the state: my code does exactly that.

Gyroscope

Earlier, I used integration so that gyroscope provided heading instead of the angular speed. This approach has a major flaw: in a real world (or in Gazebo simulation) we can not do proper integration, we simply do not have proper "previous position". So I am back to using angular velocity.

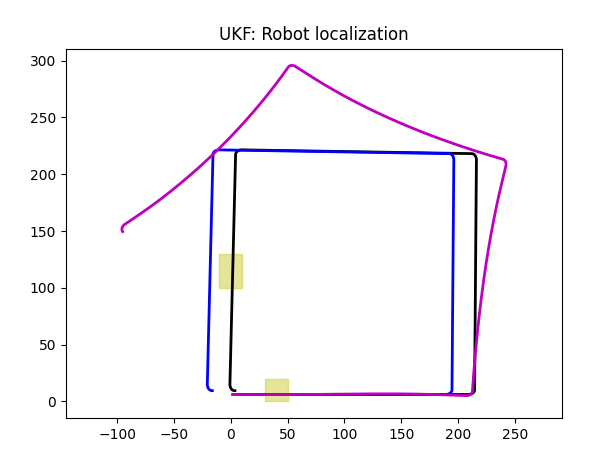
As you can see, gyroscope tries to follow the black line, as it doesn't know anything about slippage on th elinear part of a trajectory. And it has deviation - it doesn't have any way of getting coordinates, and so we have integration and errors build up.

GPS plus Gyroscope

Looks like it works, even more, the second image, if compared to pure GPS, looks "less ugly":

GPS	GPS plus Gyro

Accelerometer plus Gyroscope

What will happen if we try to use accelerometer and gyroscope together?

Kalman filter is confused and tries to average the sensor readings. In absence of "real" coordinates, integration produces data with drift. So... can we drive by inertial sensors?

We certainly can:

The last 3 charts were obtained by... reducing all parameters for both accelerometer and gyroscope 10 times. Yes, invest in a better hardware. Well...

Accelerometer plus Gyroscope plus GPS

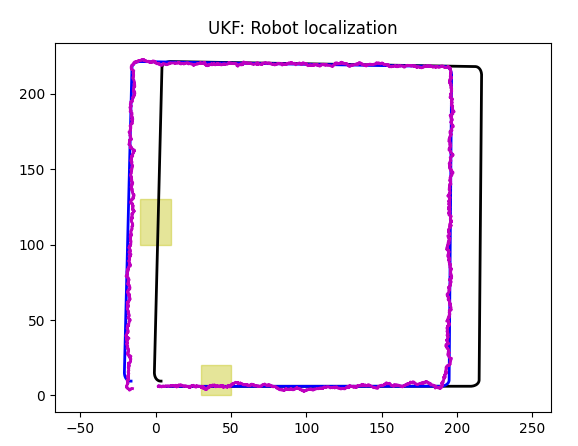
Here Kalman filter has all data it needs and result is pretty neat.

Magnetometer

Magnetometer, just like gyroscope, doesn't know anything about linear motion, but knows about rotations. As the result, Kalman draws a trajectory that is neither black nor blue. It gets velocity from command! And "drives" at that velocity, turning at angular speed of a real world robot.

Accelerometer plus Magnetometer

Here we have a picture quite similar to what we had in case of Accelerometer plus Gyroscope:

GPS plus Magnetometer

As expected, GPS provides real world coordinates, so prediction is much more accurate. Is it better than GPS alone? Not in terms of position, and as for orientation, i am going to address this issue when testing same code with Gazebo. Brief answer is "yes".

Odometer

First, let me explain what is wrong with odometer.

Odometer doesn't measure speed or coordinates directly. Instead, it calculates it based on wheel rotations. So... what if there is slippage?

Nothing. It wouldn't notice. Odometer always gives you a trajectory without any slippage.

Does that sound familiar? Yes. We already have navigation commands telling the robot where to go, and they already contain all the information odometry has, plus, it is not noisy.

So, does odometry provide us with any new info? Probably not. Instead, it will always provide us with noisy copy of "command", and you already know how hard it was to make Kalman filter to switch from non-slippage model of a command to slippage-aware model of real world.

With all that in mind, let's try out two models of Kalman odometry: first, we perform integration and provide filter with coordinates and heading; second, we provide filter with raw velocity and angular velocity.

Integrated version of Odometer

Odometer

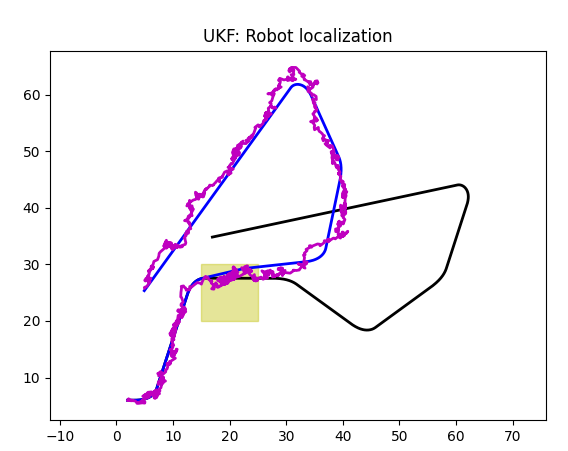
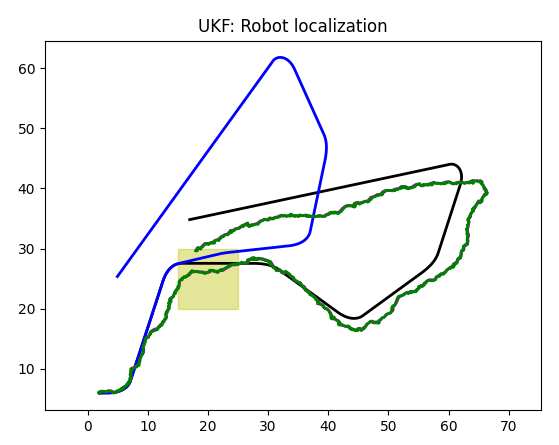
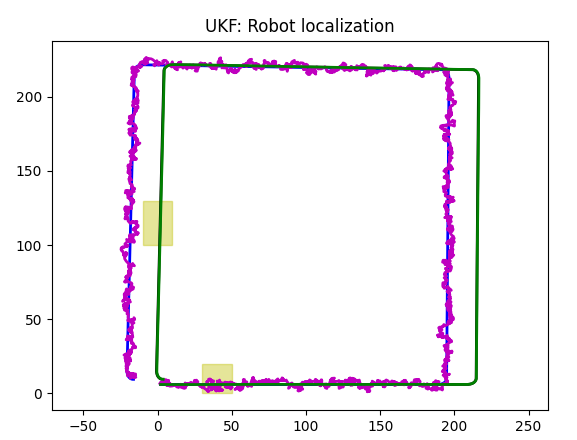
Here, black line is a trajectory without slippage, blue line is a trajectory with slippage, green line is a trajectory returned by odometer, and magenta line is a Kalman prediction. Note that magenta is hidden under green line.

As you can see, Kalman filter is trying to predict a black trajectory, and deviates due to errors.

Accelerometer plus Odometer

It gets better as accelerometer provides info that is coordinates-independent, in other words, Kalman filter doesn't have to choose between slippage-ignorant and slippage-aware worlds.

Gyroscope plus Odometer

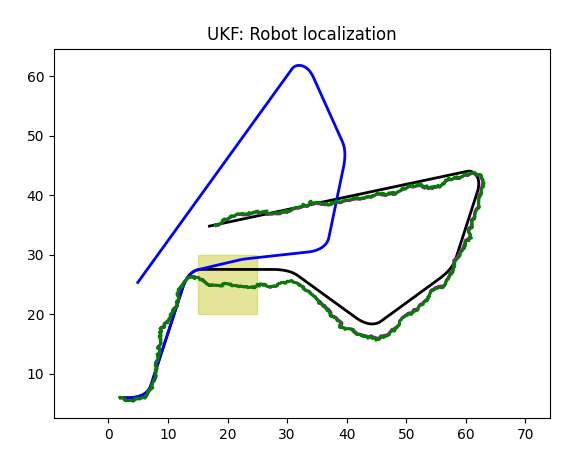
The combination of two sensors is worse than gyro but comparable to odometer. This is probably our first warning.

GPS plus Odometer

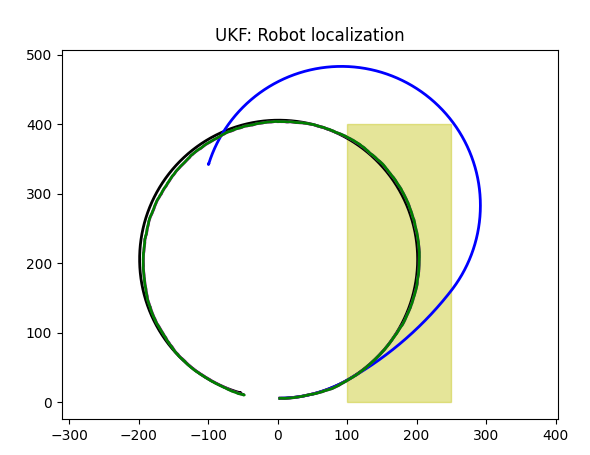
Here is the problem: odometer "suppressed" GPS sensor. We have Kalman filter that predicts black trajectory! What happened?

The problem is, odometer has data about trajectory without slippage. Commands our robot uses have the same info. So Kalman filter makes its choice in favor of non-slippery model. Which is a disaster.

Odometer without integration

Moving odometer sensor data from coordinates to velocities will increase signifficance of GPS data: will it help?

Odometer

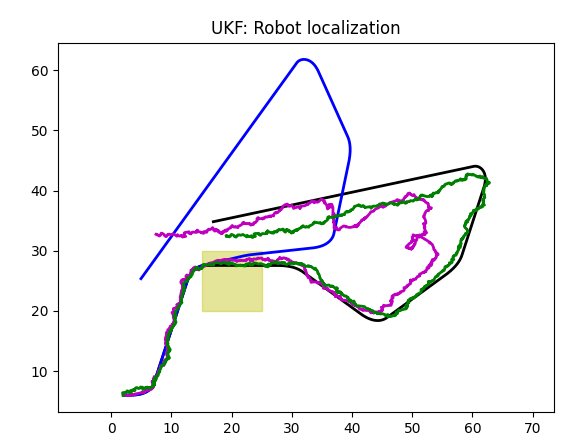
A standalone Odometer sensor is no better than an integrated version above, and probably, no worse.

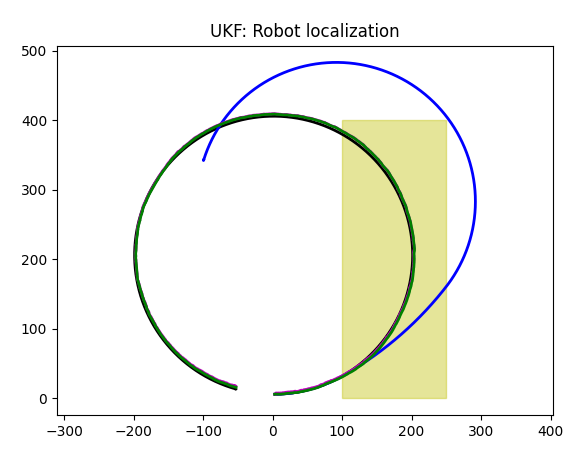
Accelerometer plus Odometer

With extra data from accelerometer, Kalman filter gets better results. The predicted trajectory follows blue line, which is what we want.

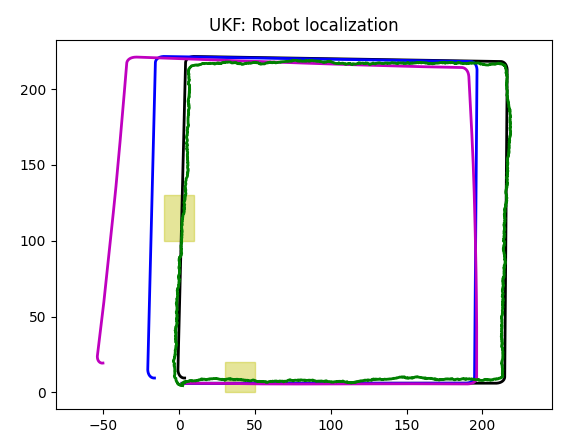
Gyroscope plus Odometer

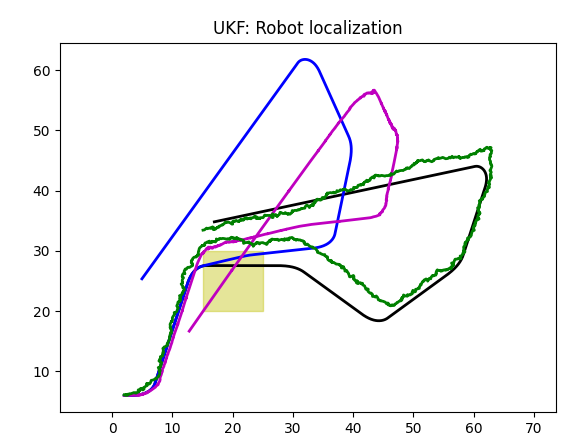
Without any data that can be linked to coordinates (gyro doesn't provide them), Kalman filter is a bit confused. More than that, on a third chart we see an artifact that is, definitely, a showstopper.

Can we do the same trick we did before: make both sensors 10 times better? Yes, but is that a realistic simulation?

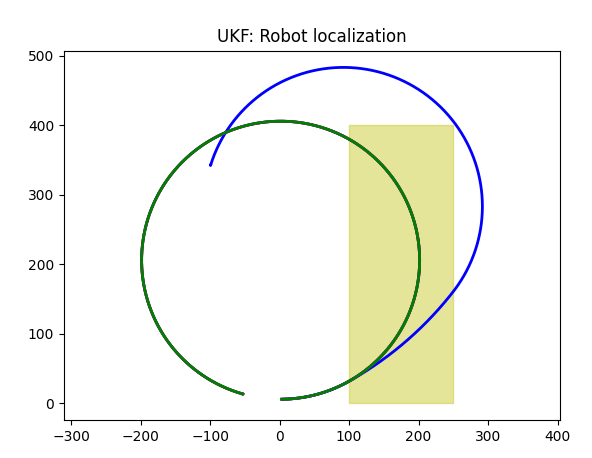
GPS plus Odometer

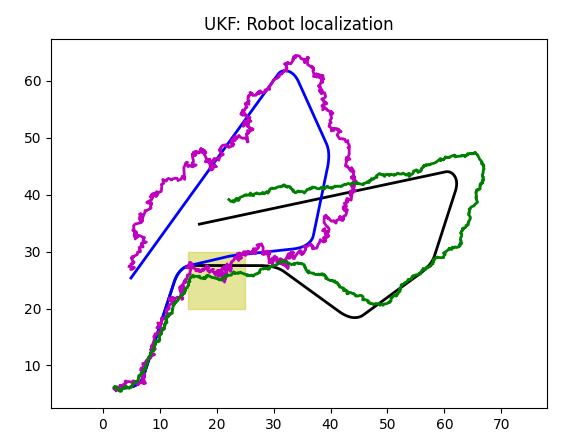
Unfortunately, our filter does same thing it did before, with integrated version: it averages, trying to combine "uncombinable" sensor data. Of course, in Kalman world there is a standard cure for that, but it is not a way to go, not in our case. Let's increase signifficance of GPS data (0.5 for first two elements of Q array, 0.2 for the third one):

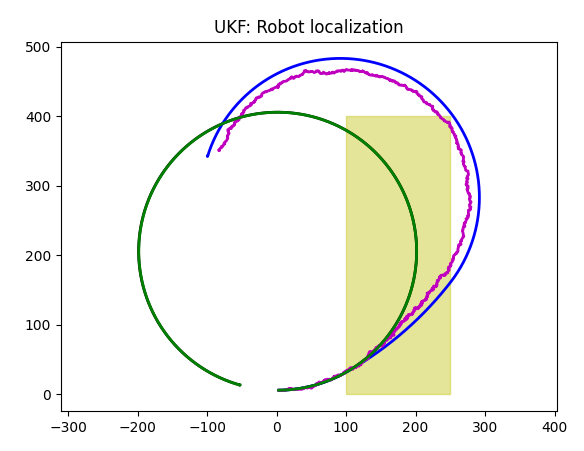
Unfortunately, Kalman filter still averages data, even though GPS has more weight.

Odometer: Conclusion

We can not use odometer in a world with slippage. While in a non-slippery world it can provide quite good results, we need to make sure there is absolutely no slippage and - just to make sure - to reset position using some other sensors, from time to time. It means we can probably use it indoor on a good non-slippery floor, but not outdoors on a mud.