First and last mile

Combining on and off road navigation

Imagine that you have parked you robot at a parking lot, next to a highway. There is a nice paved road connecting parking with a highway, and a ditch that is occupying the rest of space between them.

So far we used A Star Graph navigation algorithm on a road that had graph and if the initial position of a robot was outside the graph, well, we just used straight line navigation to get to the closest node of a graph.

There are few problems with this approach. First of all, if you drive from the parking lot to a road by a straight line, you will most likely end up in a ditch. Second, there is also a "last mile" problem, which is "drive there by a graph and then go to parking at your destination". Current implementation of our a-star navigation algorithm doesn't have this functionality. Third, we might want to drive along a highway, then do some cross-terrain driving, then highway again and so on, in other words, what if we need to randomly switch from graph based navigation to grid based navigation and back?

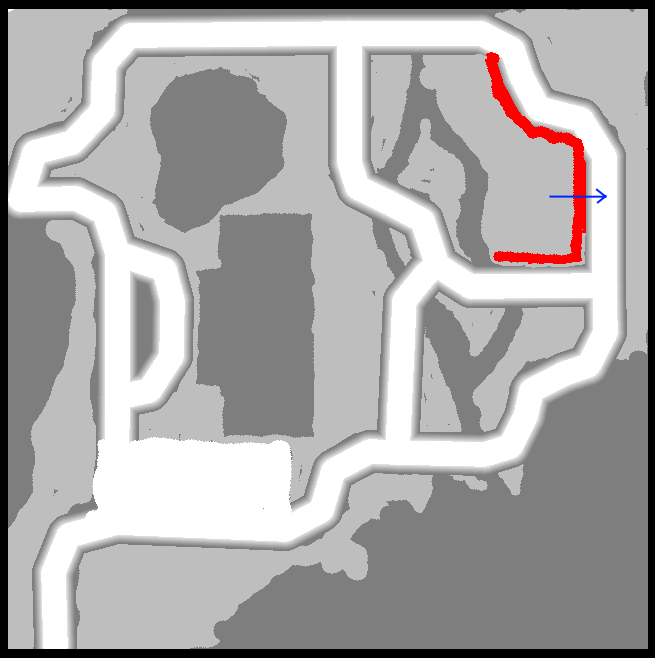
To illustrate this point I have created a wall on a keepout map. If only graph navigation algorithm is used, the robot gets to the nearest node on the road - right through the wall.

All these problems can be solved by allowing the Coordinator to decide when to use different algorithms, which means we have to make its finite automata just a bit more advanced.

As you can see on the image above, instead of going to the right, where the closest node was, the robot went down, along the "drivable" keepout level.

Using multiple colors for Path

This is not part of this section's objective, but at some point I have realized that if we have multiple waypoints, it would be convenient to draw corresponding fragments of a path between them using different colors. Of course, as we may have MANY waypoints, using too many colors is probably a bad idea, so I chose to simply switch colors. Each robot (currently, max is 2, but it is fully adjustable) has 2 colors. Path to first waypoint is painted with color_0, then color_1, then color_0 again and so on.

An obvious problem with this approach (you can see it on an image below) is that if we go to waypoint (first color) and then at least part of the way back, the second color will overwrite the first one. It can be solved by using semi-transparent colors and at some point I will probably do it.

Fragments of the path for a second robot will have different color, which helps us to distinguish them.

Coordinator.py

There are additional changes, compared to previous section. Now (and this is probably the way it should be) the Coordinator class has two planners: grid planner and graph planner. It is not user right now, but will be used soon: the idea is to use grid planner to get to the road, if the initial robot position is off the graph. Obviously, using grid planner is better than going by straight line (most likely, to the nearest ditch).

If grid planner is set to None, the straight line approach will be used.

GlobalPlannerAStarGrid.py

This is a planner that uses a-star grid algorithm. It is derived from AStar class (see earlier sections). Now, it DEFINITELY has to be also derived from GlobalPlannerStraightLine class, as it uses straight line functions. I will do it later.

Also, as we have two planners now, GlobalPlannerAStar.py is renamed to GlobalPlannerAStarGraph.py

PathFollower.py

The path follower file didn't change at all, compared to earlier section.