Kalman Filter: a REALLY brief theory

Sensors provide our robot with data (for example, it can be GPS coordinates), and these data are noisy. Top GPS sensors have accuracy within centimeters, while cheap ones most of us use (SIRF is one of them) give us something like 10 meters accuracy. Good enough to cross the desert, but not enough to cross the canyon by a narrow bridge.

Often, though not always, sensor noise has Gaussian distribution (credits to "Kalman and Bayesian Filters in Python"):

From the chart above we can see that 68% of data sensor returns are within 1 sigma (standard deviation) from the mean, 95% of data are within 2 * sigma and so on. So if we put points our GPS sensor returns for a robot that does not move, they will form a "cloud", dense in the center, and less dense as we are further from the center. If we use 1d model (for example, coordinates of a train are 1d, as it can not leave the rails), we will get points on a line (rails), more dense close to mean.

One interesting property of Gaussian is that sum of two Gaussians ia a Gaussian, and multiplication of two Gaussians is a Gaussian. After some simple math that I am going to skip (see links), we can see that the result of multiplication is less wide than each of two Gaussians we multiplied... What does it mean?

From the practical point of view, it means that if we have two sensors (or two sequential measurements by one sensor), then we can get a more "compact" cloud points representing our robot's coordinates. In other words, two sensors produce coordinates with accuracy, higher, than each sensor alone.

Another way of looking at the idea of combining data from two sensors is: if one sensor provides us with an elliptic (gaussian 2d) "spot" where 95% of data are, and another sensor provides us with it spot, then most likely (which means, another, more compact Gaussian) the true value falls into intersection of these two "spots":

And as it is a Gaussian again, we can add 3rd sensor, or 3rd sequential measurement.

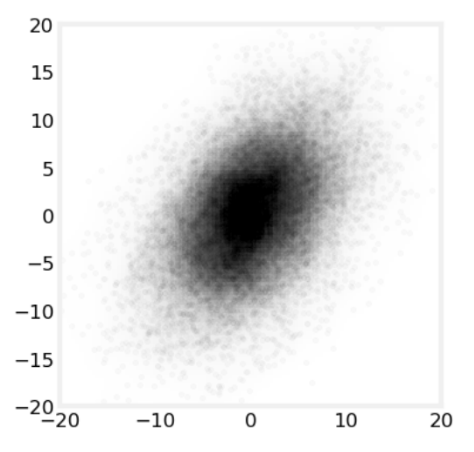
This was the base idea of a Kalman filter. However, it only works for linear dependencies. For example, if the sensor returns angle to a landmark, and to get coordinates, we need to use trigonometry (sin, cos), it is not linear anymore, and two Gaussians will produce something that is not Gaussian anymore:

Before:

After:

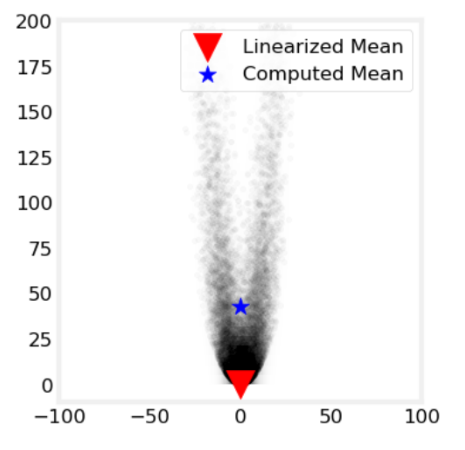
One of the ways to deal with this issue is using Unscented Kalman Filter. This is exactly what I am going to use in the sections below. A rather elegant trick is used to find points to use when calculating mean:

Unscented Kalman Filter is very easy to use - compared to alternatives. It also usually produces better results. I am going to use the library filter.py from the "Kalman and Bayesian Filters in Python" mentioned above.